Question

Try itFinding a Term of a Recursive SequencIf f(1) = 160 and f(n + 1) = -2f(n), what is f(4)?

Answer 1

We have the following recursive sequence:

`\begin{gathered} f(1)=160 \\ \\ f(n+1)=-2f(n) \end{gathered}`

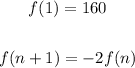
And we have to find the value for f(4) of that sequence.

To find this value, we can proceed as follows:

1. Since we have the value for the first term of the sequence, f(1) = 160, now, we can find the second term as follows:

`\begin{gathered} f(n+1)=-2f(n) \\ \\ f(1)=160 \\ \\ \text{ For n = 1, we have:} \\ \\ f(1+1)=-2f(1) \\ \\ f(2)=-2f(1)\Rightarrow f(2)=-2(160)=-320 \\ \\ \therefore f(2)=-320 \end{gathered}`

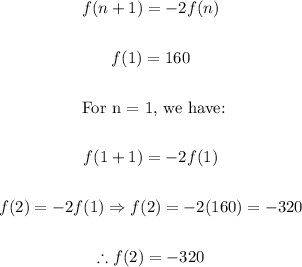
2. And now, we can proceed in a similar way to find the other two terms of the recursive sequence:

`\begin{gathered} f(n+1)=-2f(n) \\ \\ n=2 \\ \\ f(2+1)=-2f(2) \\ \\ f(3)=-2f(2)\Rightarrow f(3)=-2(-320)=640 \\ \\ \therefore f(3)=640 \end{gathered}`

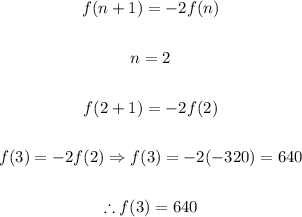
Then f(4) will be:

`\begin{gathered} f(n+1)=-2f(n) \\ \\ n=3 \\ \\ f(3+1)=-2f(3) \\ \\ f(4)=-2(640)=-1280 \\ \\ \therefore f(4)=-1280 \end{gathered}`

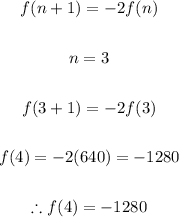
Therefore, in summary, we can conclude that f(4) = -1280