Question

Calculate the midpoints and the lengths C and I on the left

Answer 1

Midpoint: (6.5, 5.5)

Length: 1.41

Step-by-step explanation:

The midpoint of a segment with endpoints in (x1, y1) and (x2, y2) can be calculated as:

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

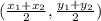
So, if the coordinates of the endpoints are point C with coordinates (7, 6) and I with coordinates (6, 5), the coordinates of the midpoint are:

`((7+6)/(2),(6+5)/(2))=(6.5,5.5)`

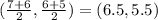
On the other hand, the distance between two points is calculated as:

`\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

So, the length of the segment that goes from C to I is equal to the distance between points C and I. Then, replacing (x1, y1) by (7, 6) and (x2, y2) by (6, 5), we get:

`\begin{gathered} \sqrt[]{(6-7)^2+(5-6)^2} \\ \sqrt[]{(-1)^2+(-1)^2} \\ \sqrt[]{1+1} \\ \sqrt[]{2}=1.41 \end{gathered}`

Therefore, the coordinates of the midpoint of segment CI are (6.5, 5.5) and the length of the segment is √2 or 1.41 units.