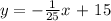Question

More linear variation

Answer 1

The two points given are (125, 10) and (150, 9)

y = number of gallons (in tanks),

x = number of miles driven

`\begin{gathered} x_1=125,y_1=10_{} \\ x_2=150,y_2=9_{} \end{gathered}`

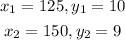
a. The rate of change = The slope =

`\text{Slope =}\frac{y_2-y_{1_{}}}{x_2-x_1}=(9-10)/(150-125)=-(1)/(25)`

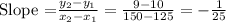
So, the rate of change is -1/25 gallon/mile (or -0.04 gallon/mile)

b. The rate of change means the amount of gallon(s) used per mile driven.

c. y-intercept is the value of y when x = 0.

From the graph, we read that y = 15 gallons when x = 0

Thus, y-intercept is 15 gallons.

d. y-intercept means the number of gallons (in tank) when zero mile is driven.

e. The equation of the line-graph is given by;

`\begin{gathered} y-y_1=slope(x-x_1) \\ \text{where x}_1=125 \\ y_1=_{}10 \\ y-10=-(1)/(25)(x-125) \\ \text{Clearing the bracket, we get} \\ y-10=-(1)/(25)x+5 \\ \text{Collecting like terms, we get} \\ y=-(1)/(25)x\text{ + 5+10} \\ \\ y=-(1)/(25)x\text{ + 15} \end{gathered}`

Hence, the equation of the graph is y = - 0.04x + 15 or

`y=-(1)/(25)x\text{ + 15}`