Question

Solve the problem down below (Round answer to four decimal places as needed)

Answer 1

Given that

We have some logarithmic values. And we have to find a log value.

Explanation -

The values that are given are

`\begin{gathered} \log_(10)2=0.3010 \\ and \\ \log_(10)36=1.5563 \end{gathered}`

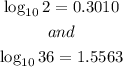
And we have to find the value of

`\log_(10)36^3=?`

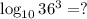
So the formula we will use here will be

`\log_(10)a^n=n*\log_(10)a`

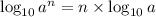
Therefore on using the formula we have

`\begin{gathered} \log_(10)36^3=3*\log_(10)36 \\ \\ substituting\text{ the value of }\log_(10)36\text{ we have} \\ \\ \log_(10)36^3=3*1.5563 \\ \log_(10)36^3=4.6689 \end{gathered}`

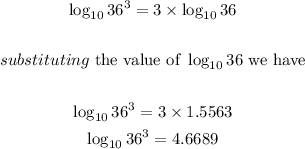
So the answer is 4.6689

Final answer -

Hence the final answer is 4.6689