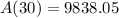Given:
Amount of money A to which a principal investment P will grow after t years at interest rate r, compounded n times per year, is given by the formula,
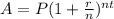
a) P= $4000, r=3% compounded daily.
The function A that models the amount to which the account grows after t years is,
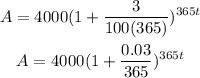
b) after 30 years the amount will be,
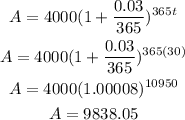
Answer: