Question

triangle ABC goes through a series of 3 transformation resulting in triangle A'B'C' the three Transformations are listed below a rotation 180 degrees clockwise about the origina reflection over the x-axisa reflection over the y-axistriangle ABC has vertex A located at ( 2,-3) using the coordinates of this point explain how the three transformation map vertex A into vertex A'

Answer 1

Step-by-step explanation:

The rule for a rotation of 180 degrees clockwise about the origin is:

`(x,y)\rightarrow(-x,-y)`

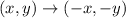
So after the first transformation, point A goes to (-2, 3)

The rule for a reflection over the x-axis is:

`(x,y)\rightarrow(x,-y)`

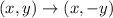
After the second transformation, point A goes to (-2, -3)

The rule for a reflection over the y-axis is:

`(x,y)\rightarrow(-x,y)`

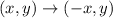
So after the last transformation, point A goes to (2, -3)

Answer:

A'(2, -3)

point A' is the same point A