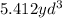1 Answer

Sarhanis · Answer 1 · 2023-08-06T14:02:52+0000

You identify that the composite figure shown in the exercise is formed by two different solids: A rectangular prism and a triangular prism.

• The surface area of a rectangular prism can be calculated with this formula:

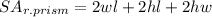
$SA_{r\text{.}prism}=2wl+2hl+2hw$

Where "l" is the length, "w" is the width and "h" is the height.

In this case, you can identify that:

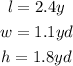
$\begin{gathered} l=2.4y \\ w=1.1yd \\ h=1.8yd \end{gathered}$

Then, substituting values into the equation and evaluating, you get:

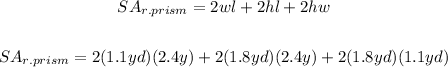
$\begin{gathered} SA_{r\text{.}prism}=2wl+2hl+2hw \\ \\ SA_{r\text{.}prism}=2(1.1yd)(2.4y)+2(1.8yd)(2.4y)+2(1.8yd)(1.1yd) \end{gathered}$
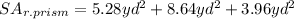
$SA_{r\text{.}prism}=5.28yd^2+8.64yd^2+3.96yd^2$
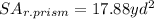
$SA_{r\text{.}prism}=17.88yd^2$

The volume of a rectangular prism can be calculated by using this formula:

$V_{r\text{.}prism}=l\cdot h\cdot w$

Where "l" is the length, "w" is the width and "h" is the height.

Since you already know its dimensions, you can substitute values into the formula and evaluate:

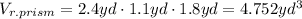
$V_{r\text{.}prism}=2.4yd\cdot1.1yd\cdot1.8yd=4.752yd^3$

• Now you need to find the surface area of the triangular prism:

$SA_{t\text{.}prism}=2B+PH$

Where "B" is the area of the base, "P" is the perimeter of the base, and "H" is the height.

In this case:

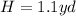
Since the bases are triangles:

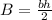
Where "b" is the base of the triangle and "h" is the height of the triangle.

Notice that:

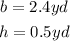
$\begin{gathered} b=2.4yd \\ h=0.5yd \end{gathered}$

Then:

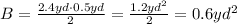
$B=(2.4yd\cdot0.5yd)/(2)=(1.2yd^2)/(2)=0.6yd^2$

To find the perimeter of the base, add the lengths of its sides:

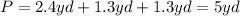
The sides of the triangle are shown below:

Therefore, knowing all these values, you can substitute them into the formula for calculating the surface area:

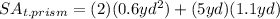
$SA_{t\text{.}prism}=(2)(0.6yd^2)+(5yd)(1.1yd)$
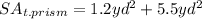
$SA_{t\text{.}prism}=1.2yd^2+5.5yd^2$
$SA_{t\text{.}prism}=6.7yd^2$

To find the volume of the triangular prism, you need to use this formula:

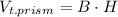
$V_{t\text{.}prism_{}}=B\cdot H$

Where "B" is the area of the triangular base and "H" is the height of the prism.

Since you already know those values, you can substitute them into the formula and evaluate:

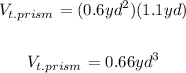
$\begin{gathered} V_{t\text{.}prism_{}}=(0.6yd^2)(1.1yd) \\ \\ V_{t\text{.}prism_{}}=0.66yd^3 \end{gathered}$

• Knowing the surface area of both solids, you have to add them in order to find the surface area of the composite figure and subtract the areas of the common faces:

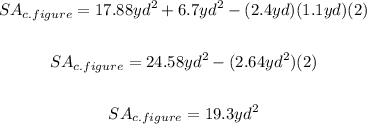
$\begin{gathered} SA_{c\text{.}figure}=17.88yd^2+6.7yd^2-(2.4yd)(1.1yd)(2) \\ \\ SA_{c\text{.}figure}=24.58yd^2-(2.64yd^2)(2) \\ \\ SA_{c\text{.}figure}=19.3yd^2 \end{gathered}$

• Knowing the volume of each solid, you need to add them in order to find the volume of the composite figure: