Question

Which of the following is the equation of an increasing exponential function?(1) y = 4(0.75)^x(2) y =7 (3/2)^x (3) y = 5x-2(4) y=4x^2

Answer 1

Let y be a general exponential function:

`y=ka^x+b`

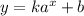
For a function to be increasing, its derivative must be positive. Notice that the derivative of this function is:

`y^(\prime)=k\cdot\ln (a)\cdot a^x`

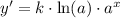
Since a^x is always positive, the sign depents only on the sign of k and ln(a).

For the product k*ln(a) to be positive, their signs must be equal. Notice that ln(a) will be positive whenever a>1, and negative whenever 0k is positive and a>1, or if k is negative and 0.

Notice that the function:

`y=7\cdot((3)/(2))^x`

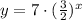
Satisfies that 7>0 and 3/2 >1. Then, it is an increasing exponential function.

Notice that the equations found in options (3) and (4) are not exponential, and the exponential function in option (1) is decreasing because 4>0 and 0<0.75<1.

Therefore, the equation in option (2) is an increasing exponential function.