Given the following equation:
![3\tan x+\sqrt[]{3}=0](https://img.qammunity.org/2023/formulas/mathematics/high-school/m2p2bd7yg2chh8v8jdfjxndk7jat25l2xv.png)
first, we can substract the square root of 3 on both sides to get:
![\begin{gathered} 3\tan x+\sqrt[]{3}-\sqrt[]{3}=0-\sqrt[]{3} \\ \Rightarrow3\tan x=-\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/g3n7kckjsysxyqwptd3cx9ckra2qbmgof6.png)
if we divide by 3 both sides of the equation, we get:
![\begin{gathered} (3\tan x=-\sqrt[]{3})\cdot(1)/(3) \\ \Rightarrow(3)/(3)\tan x=-\frac{\sqrt[]{3}}{3} \\ \Rightarrow\tan x=-\frac{\sqrt[]{3}}{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/995t56lv4bcuo4wepj2mqwlsb4tuyr7upm.png)
using the inverse of the function tangent, we can solve for x:
![\begin{gathered} \tan x=-\frac{\sqrt[]{3}}{3} \\ \Rightarrow x=\tan ^(-1)(-\frac{\sqrt[]{3}}{3})=-(\pi)/(6) \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/gsh0shc17o9waedarb5pkfdiem12ykztki.png)
since we have that x = -pi/6, but we want the values that are betwen 0 and 2 pi, we have to convert using the following expression:
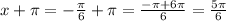
therefore, x = 5/6 pi