The function is given to be:
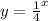
The graph of the function is shown below:
The graph is shifted up and to the left.
The graph is shifted up by 1 unit. This transformation rule is given to be:
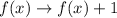
Therefore, the function becomes:
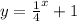
The graph is shifted to the left by 2 units. The transformation rule is given to be:
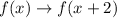
Therefore, the function becomes:
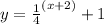
To check if the function is correct, we can use the points (-3, 5) if it gives a true statement:
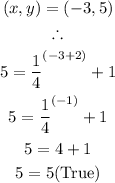
Therefore, the function is:
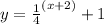
The coefficient is 1.
The exponent is x + 2.
The added constant is 1.