We are given the equation:
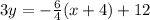
We need to solve the equation for the x-intercept. We first need to simplify the given equation into slope-intercept form.
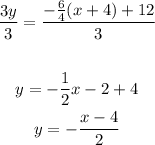
Then, we will set y = 0 and solve for x to find the x-intercept.
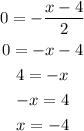
Therefore, the x-intercept is located where y = 0. This means that our coordinate pair will be (-4, 0).