Question

|2x-2|+4>12 how do I show my work for it

Answer 1

we have the inequality

`|2x-2|+4>12`

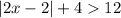
solve for x

subtract 4 both sides

`\begin{gathered} |2x-2|+4-4>12-4 \\ |2x-2|>8 \end{gathered}`

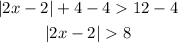
step 1

Find the first solution (positive case)

`\begin{gathered} +(2x-2)>8 \\ 2x\text{ >8+2} \\ 2x\text{ > 10} \\ x>5 \end{gathered}`

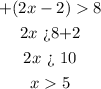
the solution of the first case is the interval (5, infinite)

step 2

Find the second solution (negative case)

`\begin{gathered} -(2x-2)>8 \\ mu\text{ltiply by -1 both sides} \\ 2x-2\text{ <-8} \\ 2x<\text{ -8+2} \\ 2x<-6 \\ x<-3 \end{gathered}`

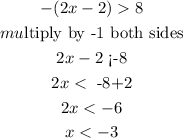
the second solution is the interval (-infinite, -3)

(-infinite, -3) ∩ (5, infinite)