Given:
Base, b = 5 cm
One side = 4 cm
Angle = 37 degrees
Let's find the area of the triangle.
To find the area of the triangle, apply the formula:
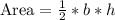
Where h is the height which was not given.
To find the height, apply trigonometric ratio formula for sine:
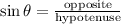
Where:
Hypotenuse = 4 cm
Opposite side is the side opposite the given angle(θ) which is the height
θ = 37 degrees
thus, we have:
![\begin{gathered} \sin 37=(h)/(4) \\ \\ \text{Multiply both sides by 4:} \\ 4(\sin 37)=(h)/(4)\ast4 \\ \\ 4(\sin 37)=h \\ \\ 4(0.602)=h \\ \\ 2.4=h \\ \\ h=2.4\operatorname{cm} \end{gathered}]()
The height of the traingle is 2.4 cm.
To find the area of the traingle, we have:
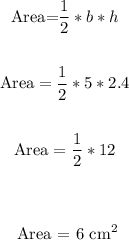
Therefore, the area of the triangle is 6 square centimeters
ANSWER:
6 cm²