Question

2 The third term of an arithmeticis 94 and The sixth term is 85Whats the 10th term

Answer 1

Given that for an Arithmetic progression:

`\begin{gathered} \text{ The third term T}_3=94 \\ \text{ The sixth term T}_6=85 \end{gathered}`

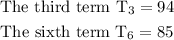
The n-th term of the sequence is given by the formula:

`\begin{gathered} U_n=U_1+(n-1)d \\ \text{where }U_1=\text{ first tem} \\ d\text{ = common difference} \end{gathered}`

Hence,

`\begin{gathered} T_3=U_1+(3-1)d=94 \\ U_1+2d=94\ldots\ldots(1) \\ T_6=U_1+(6-1)d\text{ = 85} \\ T_6=U_1+5d\text{ = 85}\ldots\ldots\text{.}(2) \end{gathered}`

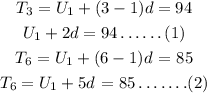
Solving both equations simultaneously using the elimination method,

`\begin{gathered} U_1+2d=94\ldots\ldots(1) \\ U_1+5d\text{ = 85}\ldots\ldots\text{.}(2) \end{gathered}`

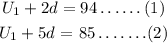
Subtract equation (2) from (1)

`\begin{gathered} 2d-5d=94-85 \\ -3d=9 \\ d=(9)/(-3) \\ d=-3 \end{gathered}`

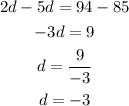
To find the first term, substitute d = -3 into equation (1)

`\begin{gathered} U_1+2d=94 \\ U_1+2(-3)=94 \\ U_1-6=94 \\ U_1=94+6 \\ U_1=100 \end{gathered}`

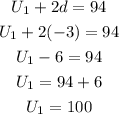
To find the 10th term of the sequence.

`\begin{gathered} T_(10)=a+(10-1)d \\ T_(10)=a+9d \\ T_(10)=100+9(-3) \\ T_(10)=100-27 \\ T_(10)=73 \end{gathered}`

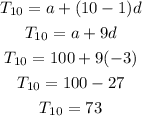
Therefore, the 10th term of the arithmetic sequence is 73