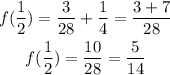Given
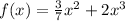
You have to calculate f(1/2) to do so, replace the formula with x=1/2
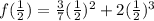
Following the order of operations, you have to solve the exponents first, then the multiplications and finally the addition.
1) Solve the exponents
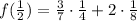
2) Solve the multiplications
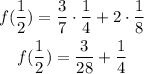
3) Solve the adition and simplify is necessary