We are given the points (1, -5) and (3,7) we are asked to determine the coordinates of the middle point. To do that we need to remember that the center of the circle is the middle point of any line segment that has end-points as diameter points. Therefore, we need to determine the middle point between these two points.
The coordinate of a middle point given the end-points of a segment is given by the following formula:
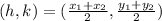
Where:
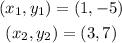
Now we substitute the values:
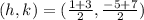
Now we solve the operations:
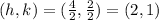
Therefore, the center of the circle is (2,1).