The expression for the magnetic force on a current lines is given by:
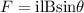
where,
i: current = 10 A
B: magnitude of the magnetic field = 0.2T
l: length of the line
θ: angle between direction of the line and the magnetic field = 90 degrees.
You can notice that the direction of the magnetic field and direction of the conduction are perpendicular, then, you have for F:
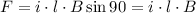
For the segment BA you obtain:
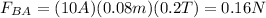
and for segment AG:
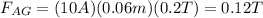
If you consider that segment BA lies on the y axis of a coordinate system and segment AG lies on x-axis (in this case BA and AG form a right angle), then, the total force on BAG is:

and its magnitude is:
![F=\sqrt[]{(0.12T)^2+(0.16T)^2}=0.2N](https://img.qammunity.org/2023/formulas/physics/college/jvsake0lfvl2yjghtizvog18v22kkhff49.png)