Given:
• Frequency, f = 1985 Hz.
,
• Speed of sound, v = 344 m/s
Let's find the distance between crests or compressions of the wave.
The distance between the crests of a wave or the compression of a wave is called the wavelength.
To find the wavelength, apply the formula:
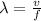
Where:
• λ is the wavelength in meters (m).
,
• v is the speed in meters per second (m/s).
,
• f is the frequency in hertz (Hz.)
Thus, we have:
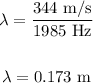
Therefore, the distance between crests or compressions of the wave is 0.173 meters.
• ANSWER:
0.173 m