Question

Solve the system by elimination or you can also use substitution. No matrices. Show all work clearly and neatly!

Answer 1

Given the system of equations:

`\begin{gathered} \begin{cases}{8-y+3z=8} \\ {3x+y_-2z{2x+4y+z=0}\end{cases}}\end{cases} \\ \\ \end{gathered}`

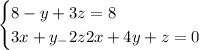
x - y + 3z = 8

3x + y - 2z = -2

2x + 4y + z = 0

Let's solve the system of equations using elimination method.

Take the first two equations:

x - y + 3z = 8

3x + y - 2z = -2

Since the y variables are opposite of each other, let's eliminate y by adding both equations:

x - y + 3z = 8

+ 3x + y - 2z = -2

__________________

4x + z = 6

Rewrite the equation for z.

Subtract 4x from both sides:

4x - 4x + z = 6 - 4x

z = 6 - 4x

Also, eliminate y in the second and third equations:

3x + y - 2z = -2

2x + 4y + z = 0

Multiply the equation 2 by -4:

-4(3x + y - 2z = -2)

2x + 4y + z = 0

-12x - 4y + 8z = 8

2x + 4y + z = 0

______________

-10x + 9z = 8

We now have the results:

4x + z = 6

-10x + 9z = 8

Multiply the top equation by -9:

-36x - 9z = -54

-10x + 9z = 8

____________

-46x = -46

x = 1

Substitute 1 for x into any of the equations:

4x + z = 6

4(1) + z = 6

z = 6 - 4

z = 2

Substitute 2 for z, and 1 for x in any equation and solve for y:

2x + 4y + z = 0

2(1) + 4y + 2 = 0

4 + 4y = 0

4y = -4

y = -1

Therefore, we have the solutions:

x = 1, y = -1, z = 2