Height:
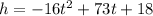
As we are asked the time when h = 91ft, then we have to set the equation to 91:
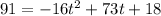
Now, we can solve for t by using the General Quadratic Equation:
![x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/li72dimqx1poek8bdg3bs589861h83kfxl.png)
in which the variables represent the coefficients of a quadratic equation in the form:

Therefore, we have to set our equation to 0:
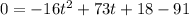
Simplifying:

Thus, in our case:
• a = -16
,
• b = 73
,
• c = 73
Replacing these values in the formula:
![t_(1,2)=\frac{-73\pm\sqrt[]{73^2-4\cdot(-16)\cdot(-73)}}{2\cdot(-16)}](https://img.qammunity.org/2023/formulas/mathematics/college/o696vjtey3is0lven61f29zsb1dg2uyoir.png)
Simplifying:
![t_(1,2)=\frac{-73\pm\sqrt[]{657}}{-32}](https://img.qammunity.org/2023/formulas/mathematics/college/mjsv7y35aw8qyyk1edgnrkapim8p875m6m.png)
![t_1=\frac{-73+3\sqrt[]{73}}{-32}\approx3.08s](https://img.qammunity.org/2023/formulas/mathematics/college/aquuckhtdgvf3jgrangplazfh04ul8uwsq.png)
![t_2=\frac{-73-3\sqrt[]{73}}{-32}\approx1.48s](https://img.qammunity.org/2023/formulas/mathematics/college/ok1ubylealx5xr7my9zwillm7rzannlm72.png)
As the object is thrown at 73ft/s, at 3 seconds it would be more or less three times higher than 73ft.
Answer: 1.48s