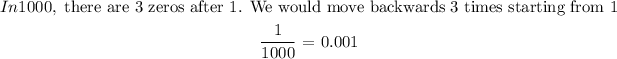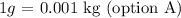Question

The mass of a paper clip is about __ kg

Answer 1

0.001 (option A)

Step-by-step explanation:

The mass of a paper clip is about 1g. We are to find the value of 1g in kg

`1000g\text{ = 1 kilogram}`

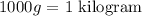
We convert from gram to kg

let the value of 1g in kg = x

1000g = 1kg

1g = x

cross multiply:

x(1000) = 1(1)

1000x = 1

divide both sides by 1000:

`\begin{gathered} (1000x)/(1000)\text{ = }(1)/(1000) \\ x\text{ = }(1)/(1000)\text{ kg} \end{gathered}`

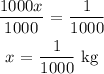
The options are in decimals we need to 1/1000 to decimal:

`\begin{gathered} In1000,\text{ there are 3 zeros after 1. We would move backwards 3 times starting from 1} \\ (1)/(1000)\text{ = 0.001} \end{gathered}`
`1g\text{ = 0.001 kg (option A)}`