Question

8x-24y = 1-x+3y = 1 How do I solve the linear equations using elimination?

Answer 1

the system has not solution

Step-by-step explanation

given

`\begin{gathered} 8x-24y=1\Rightarrow equation(1) \\ -x+3y=1\Rightarrow equation(2) \end{gathered}`

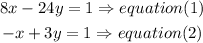
Step 1

a) mutiply equation (2) by 8 to Make the x coefficients of one variable opposites.

b) now, add the result to equation(1)

`\begin{gathered} -8x+24y=8 \\ 8x-24y\text{ }=1 \\ ........................... \\ 0=9\Rightarrow indetermination \end{gathered}`

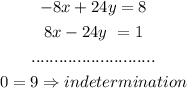
when we get a indetermination it means the system has not solution , so the answer is

the system has not solution

I hope this helps you