the lines are not parallel,and the lines are not perpendicular
Step-by-step explanation
Step 1
find the slopes
when you have two points of a line P1 and P2 you can find the slope using
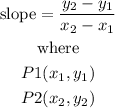
for segment AB
P1(5,6)
P2(2,2)
replace
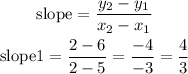
for segment CD
P1(-4,-9)
P2(-8,2)

Step 2
compare the slopes

Hence, the lines are not parallel,and the lines are not perpendicular.
I hope this helps you