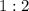Question

Find the ratio which the point (4,2) divides the line joining the points (2,-4) and (8,14).

Answer 1

Given:

The point (4, 2) divides the line joining the points (2, -4) and (8, 14).

To find: The ratio

​Explanation:

Let the ratio be,

`m:n=k:1`

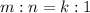
Using the section formula,

`P=\lparen(mx_2+nx_(1,))/(m+n),(my_2+ny_1)/(m+n))`

Here, we have

`\begin{gathered} m=k,n=1 \\ x_1=2,y_1=-4 \\ x_2=8,y_2=14 \end{gathered}`

On substitution we get,

`(4,2)=\lparen(8k+2)/(k+1),(14k+4)/(k+1))`

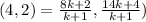
Equating the coordinates we get,

`\begin{gathered} 4=(8k+2)/(k+1) \\ 4\left(k+1\right)=8k+2 \\ 4k+4=8k+2 \\ 4k=2 \\ k=(1)/(2) \end{gathered}`

Since,

`\begin{gathered} k=(1)/(2) \\ \therefore m:n=(1)/(2):1 \\ m:n=1:2 \end{gathered}`

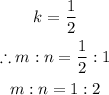
Hence, the ratio in which the point (4, 2) divides the line joining the points (2, -4) and (8, 14) is 1: 2.

Final answer: The ratio is,

`1:2`