Question

C(x) = 0.7x² – 210x+35,616

Answer 1

Quadratic Equation is represented by

`ax^2+\text{ bx + c= 0}`

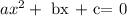
a = 0.7, b = -210, c = 35,616

Given the enormity of the values of A, B & C, we cannot solve using the factorization method. We will have to use the quadratic formula to solve

`x=\frac{-b\text{ }\pm\text{ }\sqrt{b^2-\text{ 4ac}}}{2a}`

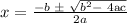
Substitute the values of a, b & c into the quadratic formula, we have:

`x=\frac{-(-210)\text{ }\pm\text{ }\sqrt{(-210^2)\text{ - 4 (}0.7\cdot\text{ 35616)}}}{2\text{ (0.7)}}`

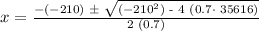
x = undefined