Question

If ΔEFG ~ ΔLMN with a ratio of 2:1, which of the following is true?Group of answer choicessegment EG is congruent to segment LMsegment EF is congruent to segment LMsegment EF over segment LM equals segment EG over segment LMsegment EF over segment LM equals segment FG over segment MN

Answer 1

Step-by-step explanation

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slid, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other.

So for

ΔEFG ~ ΔLMN

So, the congruent sides or segments will be

`\begin{gathered} segment\text{ }EG\text{ is congruent to LN} \\ segment\text{ EF is congruent to LM} \end{gathered}`

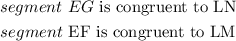
Also

`\begin{gathered} (EF)/(LM)=(EG)/(LN) \\ \\ (EF)/(LM)=(FG)/(MN) \end{gathered}`

Therefore, the answers are:

segment EF is congruent to segment LM

and

segment EF over segment LM equals segment FG over segment MN