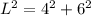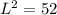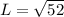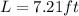Answer:
The length of the ladder is 7.21 feet
Explanation:
Let
y = Height of the wall
x = Distance between the wall and the ladder (bottom)
L = Length of the ladder
So, the given parameters are:
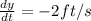
When
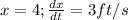
The ladder, the wall and the ground forms a right-angled triangle where the hypotenuse is the length of the ladder; So:

Differentiate with respect to time
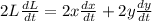
The length of the ladder does not change with time. So:
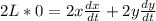
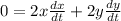
Rewrite as:
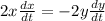
Divide both sides by 2
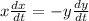
Recall that:
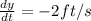 and
and
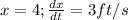
So:
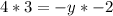
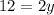
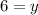
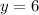
Substitute
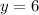 and
and
 in:
in: