ANSWER:
a. 21.2
b. 2008
Explanation:
We have that the function that models the population is the following:
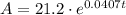
a.
In the year 2000, t = 0, we substitute and calculate the population, just like this:
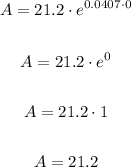
In 2000, the population of the state was 21.2 million.
b.
Now, in this case A = 29.8, we solve for t, just like this:
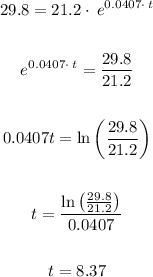
Therefore, it would be 8 years after 2000. The population of the state will reach 29.8 million in the year 2008