Question

The five number summary of a dataset is given as1,7, 12, 15, 20a. An observation is considered an outlier if it is belowb. An observation is considered an outlier if it is above

Answer 1

a. An observation is considered an outlier if it is below -5

b. An observation is considered an outlier if it is above 27

Step-by-step explanation:

Given a five-number summary of a dataset as 1,7, 12, 15, 20.

We can go ahead and label the numbers thus;

1 - Minimum

7 - 1st Quartile (Q1)

12 - Median (Middle number)

15 - 3rd Quartile(Q3)

20 - Maximum

The Interquartlie Range(IQR) = Q3 - Q1 = 15 - 7 = 8

Note that an outlier is any number less than Q1 - (1.5 * IQR) or any number greater than Q3 + (1.5 * IQR)

Let's now determine the value of Q1 - (1.5 * IQR) as seen below;

`7-(1.5\cdot8)=7-12=-5`

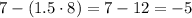
Therefore, an observation is considered an outlier if it is below -5

Let's now determine the value of Q3 + (1.5 * IQR) as seen below;

`15+(1.5\cdot8)=15+12=27`

Therefore, an observation is considered an outlier if it is above 27