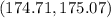Given the following parameters

To find the mean of the data, we will have to use
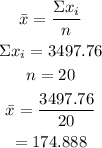
Using the confidence interval formula of
![CI=\bar{x}\pm z_{(\alpha)/(2)}*\frac{\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/tekr2a84hl2mywyq3699j12pl3w64cf6me.png)
Substitute for all values to find the confidence interval.
![\begin{gathered} CI=174.888\pm1.960*\frac{0.4}{\sqrt[]{20}} \\ =174.888\pm1.960*0.0894427191 \\ =174.888\pm0.175 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/wy9pjm7bnxdtwbh3h2zptauk6d395em1bp.png)
Hence, the confidence interval is
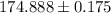
The critical value is
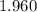
The standard error of the mean is
![\sigma_{\bar{x}}=\frac{\sigma}{\sqrt[]{n}}=\frac{0.4}{\sqrt[]{20}}=0.089](https://img.qammunity.org/2023/formulas/mathematics/high-school/at9h4nxp5mr74520xti4kfsiqgdrqmh0nb.png)
The confidence interval is