Question

if you are dealt 4 cards from a shuffled deck of 52 cards, find the probability of getting one Queen and three king​

Answer 1

Answer:
`(16)/(270725)`

This is the same as writing 16/270725

========================================================

Step-by-step explanation:

There are 4 ways to draw a queen and 4 ways to select three kings (think of it like saying there are 4 ways to leave a king out). That produces 4*4 = 16 ways total to draw the four cards we want.

This is out of
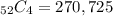`_(52)C_4 = 270,725` ways to select four cards without worrying if we got a queen and/or king. The steps to finding this number are shown below.

Divide the two values found to get the final answer
`(16)/(270725)`

--------------------

Scratch Work:

Computing the value of
`_(52)C_4`

Plug in n = 52 and r = 4 into the combination formula below

`_(n) C _(r) = (n!)/(r!*(n-r)!)\\\\_(52) C _(4) = (52!)/(4!*(52-4)!)\\\\_(52) C _(4) = (52*51*50*49*48!)/(4!*48!)\\\\_(52) C _(4) = (52*51*50*49)/(4!) \ \ \text{ .... the 48! terms cancel}\\\\_(52) C _(4) = (52*51*50*49)/(4*3*2*1)\\\\_(52) C _(4) = (6,497,400)/(24)\\\\_(52) C _(4) = 270,725\\\\`

We use the nCr combination formula (instead of the nPr permutation formula) because order doesn't matter with card hands.