Question

The population of wild elephants in the world is 400,000. Each year, the population of elephantsdecreases 6%. How many wild elephants will be left in the world in 10 years? Show your work andhow you entered it into the formula. Shint: Use y = a(1 - r)^x

Answer 1

We can model this situation with an initial population a=400,000.

The rate of change of the population is -6%, so the population at year x=1 will be:

`y(1)=400,000\cdot(1-0.06)=400,000\cdot0.94=376,000`

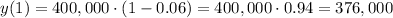
The second year (x=2), the population will decrease another 6%:

`y(2)=376,000\cdot0.94=353,440=400,000\cdot(1-0.06)^2`

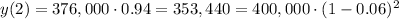
We can generalize this as:

`y(x)=400,000\cdot(1-0.06)^x`

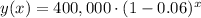
Then, ten years from now (x=10), the population will be:

`y(10)=400,000\cdot(1-0.06)^(10)\approx400,000\cdot0.5386\approx215,446`

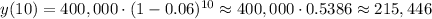
The expected population 10 years from now is 215,446 elephants.