We can take
That is, x be the length and and the width of the rectangle. So we have the following system of linear equations:
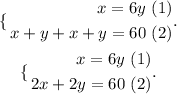
Since to obtain the perimeter all the sides of the rectangle must be added.
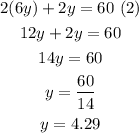
Now that we have the value of y we can plug it into equation (1)
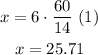
Finally, the dimensions of the rectangle are 25.7 cm long and 4.3 cm wide.