To answer this question, we can use the Pythagorean Theorem twice to find a side of the shared side of both triangles, and then to find the side x.
Finding the measure of the shared side
We can apply the Pythagorean Theorem as follows:
![h^2=15^2+20^2\Rightarrow h^2=225+400\Rightarrow h^2=625\Rightarrow\sqrt[]{h^2}=\sqrt[]{625}\Rightarrow h=25](https://img.qammunity.org/2023/formulas/mathematics/college/pi1pqks71wwvbs5p4fm3fjw5al3tyrglmi.png)
Therefore, the shared side measures 25 units. With this side, then, we can find the side h (hypotenuse) of the other triangle also using the Pythagorean Theorem:
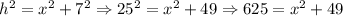
Then, we have, subtracting 49 to both sides of the equation:
![625-49=x^2+49-49\Rightarrow576=x^2\Rightarrow\sqrt[]{x^2}=\sqrt[]{576}\Rightarrow x=24](https://img.qammunity.org/2023/formulas/mathematics/college/wjyn485deksnrte461tgw4uzf2riktor2q.png)
Therefore, the value for x is equal to 24 units (second option).