Question

Which line is perpendicular to 3y + 2x = 12?A. 6x - 4y = 24C. 2x + 3y = 6B. y + 3x = -2D. y = -2x + 6

Answer 1

We are asked that which line is perpendicular to the following equation.

`3y+2x=12`

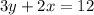
First of all, we have to convert this equation into the slope-intercept form so that we can identify it's slope.

`\begin{gathered} 3y+2x=12 \\ 3y=-2x+12 \\ y=(-2x)/(3)+(12)/(3) \\ y=(-2x)/(3)+4 \end{gathered}`

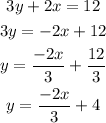
Recall that the standard slope-intercept form is given by

`y=mx+b`

Where m is the slope and b is the y-intercept.

So comparing the standard form with the above equation, we find that

`m_1=(-2)/(3)`
`b=4`

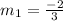
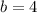
Now recall that the slopes of two perpendicular lines are negative reciprocals of each other.

`m_1=-(1)/(m_2)`

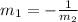
Therefore, the line perpendicular to the given equation will have a slope of

`m_2=(3)/(2)`

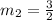
Finally, now we will check which given option has the exact above slope, that will be the correct equation.

Option A:

`\begin{gathered} 6x-4y=24 \\ -4y=-6x+24 \\ y=(6x)/(4)-(24)/(4) \\ y=(3)/(2)x-6 \end{gathered}`

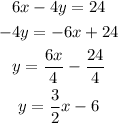
This is the equation we were looking for since it has the slope m = 3/2

Therefore, the correct option is A.

The line 6x - 4y = 24 is perpendicular to the line 3y + 2x = 12