Question

The coefficient of variation CV describes the standard deviation as a percent of the mean. Because it has no units, you can use the coefficient of variation to compare data with different units. Find the coefficient of variation for each sample data set. What can you conclude?CV=(standard deviation/mean)*100

Answer 1

The coefficient of variation CV is a relative measure of variation, as mentioned in the text, it describes the variability of the sample as a percentage of the mean.

To calculate the coefficient of variation you have to use the following formula:

`CV=\frac{S}{X_{\text{bar}}}\cdot100`

Where

CV is the coefficient of variation

S is the sample standard deviation

Xbar is the sample mean

Given the data sets of heights and weights, to determine the CV of each sample, you have to calculate the mean value and standard deviation of them.

To calculate the mean value of a sample you have to use the following formula:

`X_{\text{bar}}=(\Sigma x)/(n)`

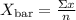
Where

∑x is the sum of each observation

n is the total number of observations

To calculate the standard deviation you have to calculate the variance of the sample and then calculate its square root.

The formula for the variance is

`S^2=(1)/(n-1)\lbrack\Sigma x^2-((\Sigma x)^2)/(n)\rbrack`

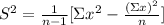
And the standard deviation is

`S=\sqrt[]{S^2}`

Where

∑x² is the sum of squares of the observations

∑x is the sum of each observation

n is the total number of observations

1) Heights:

There is a total of 12 heights recorded in the table, so the sample size is n₁=12

Before calculating the mean and standard deviation you have to calculate the sum and sum of squares of the heights.

`\begin{gathered} \Sigma x_1=76+70+68+73+68+78+71+69+72+73+76+65 \\ \Sigma x_1=859 \end{gathered}`
`\begin{gathered} \Sigma x^2_1=76^2+70^2+68^2+73^2+68^2+78^2+71^2+69^2+72^2+73^2+76^2+65^2 \\ \Sigma x^2_1=61653 \end{gathered}`

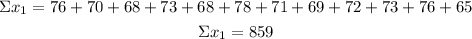
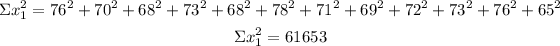
Mean (xbar₁)

`\begin{gathered} X_{\text{bar}1}=(\Sigma x_1)/(n_1) \\ X_{\text{bar}1}=(859)/(12) \\ X_{\text{bar}1}=71.58 \end{gathered}`

Variance (S₁²)

`\begin{gathered} S^2_1=(1)/(n_1-1)\lbrack\Sigma x^2_1-\frac{(\Sigma x_1)_{}^2}{n}\rbrack \\ S^2_1=(1)/(12-1)\lbrack61653-(859^2)/(12)\rbrack \\ S^2_1=(1)/(11)\lbrack61653-61490.0.83\rbrack \\ S^2_1=14.81 \end{gathered}`

Standard deviation (S₁)

`\begin{gathered} S_1=\sqrt[]{S^2_1} \\ S_1=\sqrt[]{14.81} \\ S_1=3.85 \end{gathered}`

Coefficient of variation (CV₁)

`\begin{gathered} CV_1=\frac{S_1}{X_{\text{bar}1}}\cdot100 \\ CV_1=(3.85)/(71.58)\cdot100 \\ CV_1=5.38 \end{gathered}`

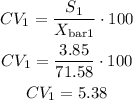
2)Weights

There is a total of 12 weights on the table, so the sample size is n₂=12

As before, to calculate the mean and standard deviation you have to calculate the sum and sum of squares of the 12 weights:

`\begin{gathered} \Sigma x_2=203+169+194+208+207+193+165+226+225+206+168+186 \\ \Sigma x_2=2350 \end{gathered}`
`\begin{gathered} \Sigma x^2_2=203^2+169^2+194^2+208^2+207^2+193^2+165^2+226^2+225^2+206^2+168^2+186^2 \\ \Sigma x^2_2=464950 \end{gathered}`

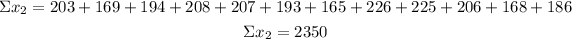
Mean (xbar₂)

`\begin{gathered} X_{\text{bar}2}=(\Sigma x_2)/(n_2) \\ X_{\text{bar}2}=(2350)/(12) \\ X_{\text{bar}2}=195.83 \end{gathered}`

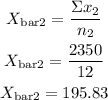
Variance (S₂²)

`\begin{gathered} S^2_2=(1)/(n_2-1)\lbrack\Sigma x^2_2-((\Sigma x_2)^2)/(n_2)\rbrack \\ S^2_2=(1)/(12-1)\lbrack464950-((2350)^2)/(12)\rbrack \\ S^2_2=(1)/(11)\lbrack464950-460208.33\rbrack \\ S^2_2=431.06 \end{gathered}`

Standard deviation (S₂)

`\begin{gathered} S_2=\sqrt[]{S^2_2} \\ S_2=\sqrt[]{431.06} \\ S_2=20.76 \end{gathered}`

Coefficient of variation (CV₂)

`\begin{gathered} CV_2=\frac{S_2}{X_{\text{bar}2}}\cdot100 \\ CV_2=(20.76)/(195.83)\cdot100 \\ CV_2=10.60 \end{gathered}`

The coefficient of variation of the heights CV₁=5.4% is significantly smaller than the coefficient of variation of the weights CV₂=10.60%, which indicates that the data set of the heights have less variability than the data set of the weights.