Let:
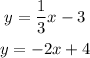
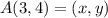
Let's evaluate the point into the line 1:
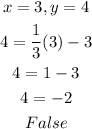
Therefore, the point is not on the line 1.
The algebraic representation is:
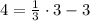
------------------------------
Let's evaluate the point into the line 2:
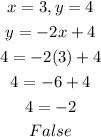
Therefore, the point is not on the line 2.
The algebraic representation is:
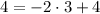
The point is not a solution for both equations