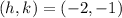Question

X^2 + 4X + Y^2 + 2Y = -2 rewrite it in a standard form. find the its radius and coordinates of its center

Answer 1

To solve the exercise, we are going to complete the square, that is, we are going to find values c and d, such that these polynomials:

`\begin{gathered} x^2+4x+c \\ \text{ and} \\ y^2+2y+d \end{gathered}`

be perfect square trinomials.

These values are found like this:

`\begin{gathered} c=((b)/(2))^2 \\ \text{ Where} \\ ax^2+bx+c\Rightarrow\text{ Square trinomial} \end{gathered}`

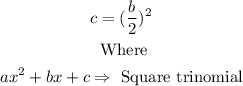
Then the value c will be:

`\begin{gathered} x^2+4x+c \\ a=1 \\ b=4 \\ c=\text{?} \\ c=((b)/(2))^2 \\ c=((4)/(2))^2 \\ c=2^2 \\ c=4 \end{gathered}`

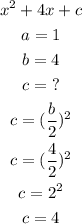
And the value d will be:

`\begin{gathered} y^2+2y+d \\ a=1 \\ b=2 \\ d=\text{?} \\ d=((b)/(2))^2 \\ d=((2)/(2))^2 \\ d=1^2 \\ d=1 \end{gathered}`

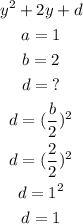
Now, rewriting the original equation:

`\begin{gathered} x^2+4x+y^2+2y=-2 \\ x^2+4x+y^2+2y+c+d=-2+c+d \\ \text{ Add c and d to both sides of the equation so as not to alter the equality} \\ x^2+4x+y^2+2y+4+1=-2+4+1 \\ \text{ Add similar terms} \\ x^2+4x+y^2+2y+4+1=3 \\ \text{ Reorder} \\ x^2+4x+4+y^2+2y+1=3 \\ \text{ Factor} \\ (x+2)^2+(y+1)^2=3 \end{gathered}`

Now, the equation of a circle in standard form is

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ \text{ Where} \\ (h,k)\text{ are the coordinates of the center and} \\ r\text{ is the radius of the circle} \end{gathered}`

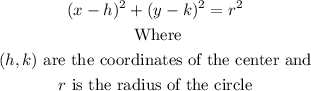
Therefore, the equation of this circle in its standard form is

`(x+2)^2+(y+1)^2=3`

the radius is

`\begin{gathered} r=\sqrt[]{3} \\ \text{ Because} \\ r^2=(\sqrt[]{3})^2=3 \end{gathered}`

the coordinates of the center are

`\begin{gathered} h=-2 \\ \text{ Because} \\ (x+2)^2=(x-(-2))^2=(x-h)^2 \\ \text{ and} \\ k=-1 \\ \text{ Because} \\ (y+1)^2=(y-(-1))^2=(y-k)^2 \end{gathered}`

and the center is

`(h,k)=(-2,-1)`