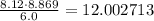For point a. Write the numbers one below the other, lining up the decimal points. If necessary add zeros so that both numbers have the same number of digits.

Add each column of digits, starting from the right and going to the left. If the result of adding a column is more than 10, digits can be moved to the next column on the left.

For point b. You can first apply the associative property of multiplication, that is
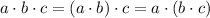
Then you have
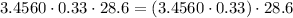
Now to multiply decimals, multiply without the decimal point and then put the decimal point like this as follows

So, you have
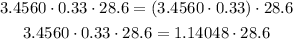

Therefore,
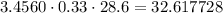
For point c. First, perform the subtraction, which is the operation within the parentheses, and then perform the addition. To subtract decimal numbers, proceed in the same way as with the addition of decimal numbers, with the difference that if the digit you are trying to subtract is greater than the digit that is above it, you can borrow a digit from the column of the left.

Now adding
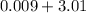
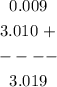
Therefore,
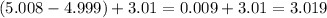
For point d. First, you can make the product that is in the numerator and then do the division. Then, you have

Now dividing

Therefore,