The form of the linear equation is

m is the slope
b is the y-intercept (initial value at x = 0)
Since the cost is C and the number of dances is L, then
The equation should be

We will use the given information to find m and b
Since 7 lessons cost $82 dollars, then
Substitute C by 82 and L by 7
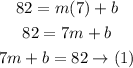
Since 11 lessons cost $122, then
Substitute C by 122 and L by 11

Now, we have a system of equations to solve it
Subtract equation (1) from equation (2) to eliminate b

Divide both sides by 4 to find m
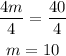
Substitute m in equation (1) by 10 to find b
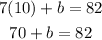
Subtract 70 from both sides to find b
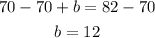
The equation of the cost of L lessons is
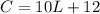
If the number of the lessons is 4, then substitute L by 4 to find the cost
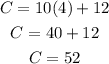
The cost of the 4 lessons is $52
11. C = 10L + 12
12. $52