Consider the equation:x^2 = -8x – 71) Rewrite the equation by completing the square.Your equation should look like (x + c)^2 = d or (x – c)^2 = d.

Question

asked Dec 18, 2023 119k views

1 Answer

Mark Rhodes · Answer 1 · 2023-12-22T00:33:40+0000

First we rewrite it to have an equation equal to zero:

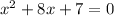
To complete the square we have to consider that a perfect square looks like:

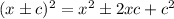
$(x\pm c)^(2)=x^2\pm2xc+c^2$

In this equation we have in the second term 8x, so comparing it to the perfect square we have that c must be 4:

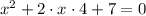
$x^2+2\cdot x\cdot4+7=0$

If the last term of a perfect square is c², we should have 16 instead of 7. To complete the square we have to add and substract 16:

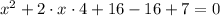
$x^2+2\cdot x\cdot4+16-16+7=0$

Note that if we do that the equation remains the same.

Now if we look at the first 3 terms we can see a perfect square:

$\begin{gathered} (x^2+2\cdot x\cdot4+16)-16+7=0 \\ (x+4)^(2)-9=0 \end{gathered}$

And now we add 9 on both sides of the equation:

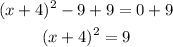
$\begin{gathered} (x+4)^2-9+9=0+9 \\ (x+4)^2=9 \end{gathered}$

The equation rewritten in complete square form is (x + 4)² = 9