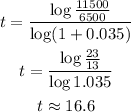ANSWER
t = 16.6
Step-by-step explanation
In the formula:
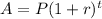
A is the final amount, in this case is 11500 people. P is the initial amount, in this case is 6500 people. r is the growth rate, which in this case is 0.035 - we have to express it as a decimal, not a percent. And finally t is the time, which is the variable we want to find.
Let's clear t first and replace all these values at the end. To clear t we have to leave only the factor which exponent is t on one side of the equation. To do this we have to divide both sides by P:
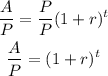
Now we have to use the following rule for the exponents and logarithms:

For this problem we have:
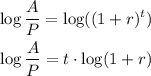
Now we have to divide both sides by log(1+r) to clear t:
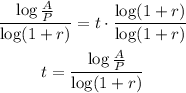
And finally we just have to replace the values into this equation we found: A = 11500, P = 6500 and r = 0.035: