To answer this question, we will use the following formula:
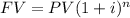
Where we identify the following components :
* FV= Future Value ( In this question, FV=8140)
*PV= Present Value (In this question PV= 5500)
* i = Interest rate ( In this question i=? Unknown)
*n= Number of periods compounded.
We have to take care to calculate n, we know that is the quantity of times that the interest rate is compound, we also know that the duration is 7 years, but we have to count the times in terms of the period on which the interest rate is compounded.
In this question, the interest rate is compounded quarterly; therefore we have to find, how many quarters are in seven years? Since each year has 4 quarters, we find that

We conclude n=28, now we can solve for i (the interest rate) the first equation presented above:
![\begin{gathered} 8140=5500(1+i)^(28) \\ (8140)/(5500)=(1+i)^(28) \\ \sqrt[28]{(8140)/(5500)}-1=i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2y6c6p4na2camhpme76735xo1gnh03bce1.png)
Calculating the left hand side term on the last line of the equation above, we find that:
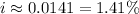
We conclude that the interest rate of this operation is 1.41%