Question

Recall the equation for a circle with center (h,k) and radius r . At what point in the first quadrant does the line with equation y=1.5x+5 intersect the circle with radius 4 and center (0, 5)?

Answer 1

The form of the equation of the circle is

`(x-h)^2+(y-k)^2=r^2`

(h, k) is the center

r is the radius

Since the given center is (0, 5) and the given radius is 4, then

The equation of the circle is

`\begin{gathered} (x-0)^2+(y-5)^2=16 \\ x^2+(y-5)^2=16\rightarrow(1) \end{gathered}`

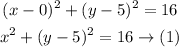
Since the equation of the line is

`y=1.5x+5\rightarrow(2)`

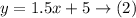
Substitute y in equation (1) by equation (2)

`\begin{gathered} x^2+(1.5x+5-5)^2=16 \\ x^2+(1.5x)^2=16 \\ x^2+2.25x^2=16 \end{gathered}`

Add the like terms on the left side

`3.25x^2=16`

Divide both sides by 3.25

`\begin{gathered} (3.25x^2)/(3.25)=(16)/(3.25) \\ x^2=(64)/(13) \end{gathered}`

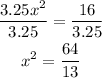
Take a square root for both sides

`\begin{gathered} √(x^2)=\sqrt{(64)/(13)} \\ x=2.218800785 \end{gathered}`

Substitute the value of x in equation (2) to find y

`\begin{gathered} y=1.5(2.218800785)+5 \\ y=8.328201177 \end{gathered}`

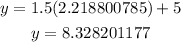
Round them to 3 decimal places

x = 2.219

y = 8.328