Question

Solve the equation using elimination. 3x-4y=9-3x+2y = 9.

Answer 1

(-9, - 9)

Explanation:

Given information

3x - 4y = 9 ---------- equation 1

-3x + 2y = 9 ---------- equation 2

The above systems of the equation can be solved simultaneously by using the elimination method

Firstly, to the variable x. To do this, we need to add equations 1 and 2 together

`\begin{gathered} \lbrack3x\text{ + (-3x)\rbrack + (-4y + 2y) = 9 + 9} \\ (3x\text{ - 3x ) - 2y = 18} \\ 0\text{ - 2y = 18} \\ -2y\text{ = 18} \\ \text{Divide both sides by -2} \\ \frac{\cancel{-2}y}{\cancel{-2}}\text{ = }\frac{\cancel{18}9}{\cancel{-2}} \\ y\text{ = }-9 \end{gathered}`

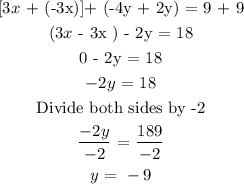
The value of y = -9

Now, can now find the value of x by substituting x = -9 in equation 1

`\begin{gathered} 3x\text{ - 4y = 9} \\ 3x\text{ - 4(-9) = }9 \\ 3x\text{ + 36 = 9} \\ \text{subtract 36 from both sides} \\ 3x\text{ + 36 - 36 = 9 - 36} \\ 3x\text{ = -27} \\ \text{Divide both sides by 3} \\ \frac{\cancel{3}x}{\cancel{3}}\text{ = }\frac{\cancel{-27}\text{ -9}}{\cancel{3}} \\ x\text{ = -9} \end{gathered}`

Therefore, x = -9 and y = -9

(-9,-9)