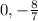Given:
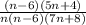
Required:
We need to find the excluded values of the domain.
Step-by-step explanation:
Cancel out the common factor (n-6).
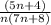
The excluded points can be found by equating the numerator of the given expression equal to zero.
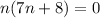
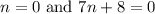
We get n =0 is one of the excluded points
Consider the equation 7n+8=0.
Subtract 8 from both sides.
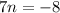
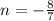
n=-8/7 is the second excluded point.
Final answer:
The excluded values are