Question

7. You want to be able to withdraw the specified amount periodically from a payout annuity with the given terms. Find how much the account needs to hold to make this possible. Round your answer to the nearest dollar. Regular withdrawal: $2100 Interest rate: 2% Frequency weekly Time: 19 years Account balance: $

Answer 1

Use the payout annuity formula.

`P_0=(d(1-(1+(r)/(k))^(-Nk)))/(((r)/(k)))`

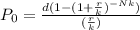
The weekly withdrawl is $2100 so d=$2100

Each year has around 52 weeks so number of periods is k=52.

The interest rate is 2% per annum so r=0.02

The number of years is 19 so N=19.

So it follows:

`\begin{gathered} P_0=(2100(1-(1+(0.02)/(52))^(-19*52)))/((0.02)/(52)) \\ P_0=1725843.905 \end{gathered}`

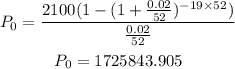
Hence you should have $1725843.905 in your bank account to pay yourself $2100 a week for 19 years if the account earns 2% per annum.