Question

The floor of a storage unit is 6 feet long and 6 feet wide. Starting at the far left corner, Rob walks down the length, across the width, and then diagonally back to the far left corner. How far does Rob walk? If necessary, round to the nearest tenth.

Answer 1

we draw a picture

red line is the Rob's road traveled 6ft, 6ft and diagonal

we can calculate the diagonal using pythagoras because the shape of the walk is a right triangle

`a^2+b^2=h^2`

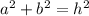
where a and b are legs of the triangle and h the hypotenuse, replacing the values of the legs

`6^2+6^2=d^2`

simplify

`\begin{gathered} 36+36=d^2 \\ 72=d^2 \end{gathered}`

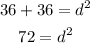
and solve for diagonal

`\begin{gathered} d=\sqrt[]{72} \\ d=6\sqrt[]{2} \end{gathered}`

now sum the walked sides

`\begin{gathered} 6+6+6\sqrt[]{2} \\ =12+6\sqrt[]{2}\approx20.5 \end{gathered}`

Rob walks 20.5 feet