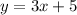Question

Write the equation of a line with a slope of 3 that passes through (-4,-7)

Answer 1

The equation of the line with a slope of 3 that passes through (-4,-7) is;

`y=3x+5`

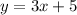
Step-by-step explanation:

We want find the equation of the line with;

`\begin{gathered} \text{Slope m}=3\text{ } \\ \text{ passing through point }(x_1,y_1)\rightarrow(-4,-7) \end{gathered}`

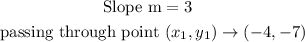
Using the point slope form of linear equation;

`y-y_1=m(x-x_1)`

substituting the given values into the equation above we have;

`\begin{gathered} y-(-7)=3(x-(-4)) \\ y+7=3(x+4) \end{gathered}`

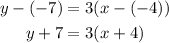
Above is a point slope form of the equation.

solving further we have;

`\begin{gathered} y+7=3x+12 \\ y+7-7=3x+12-7 \\ y=3x+5 \end{gathered}`

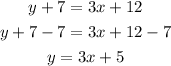
The equation of the line with a slope of 3 that passes through (-4,-7) is;

`y=3x+5`