Step 1
If the average cost of the items produced = 39
Then,
The cost to produce the items should not be more than 39x
Therefore,

Step 2
Simplify and get the final answer
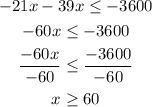
Therefore the least number of items that can be produced so that the average cost is no more than $39 = 60 items